I have the same issue. New MacBook Pro 13' 16GB RAM, 1TB SSD, After installing Big Sur I need to reset MacBook 2-3 times a day. Previously on Catalina, my computer was up over 100 days without resetting. WIN one of 10 Mac in a Sac Polar down jackets worth £79.99! Amabel Buck 25th January 2019 We’ve got together with the guys at Mac in a Sac to bring you the chance to win.
- 2.3 Discover The Slope Of A Linemr. Mac's Page Sheet
- 2.3 Discover The Slope Of A Linemr. Mac's Page Login
Graph a Line Given a Point and the Slope
In this chapter, we graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.
Another method we can use to graph lines is the point-slope method. Sometimes, we will be given one point and the slope of the line, instead of its equation. When this happens, we use the definition of slope to draw the graph of the line.
Example (PageIndex{11}):
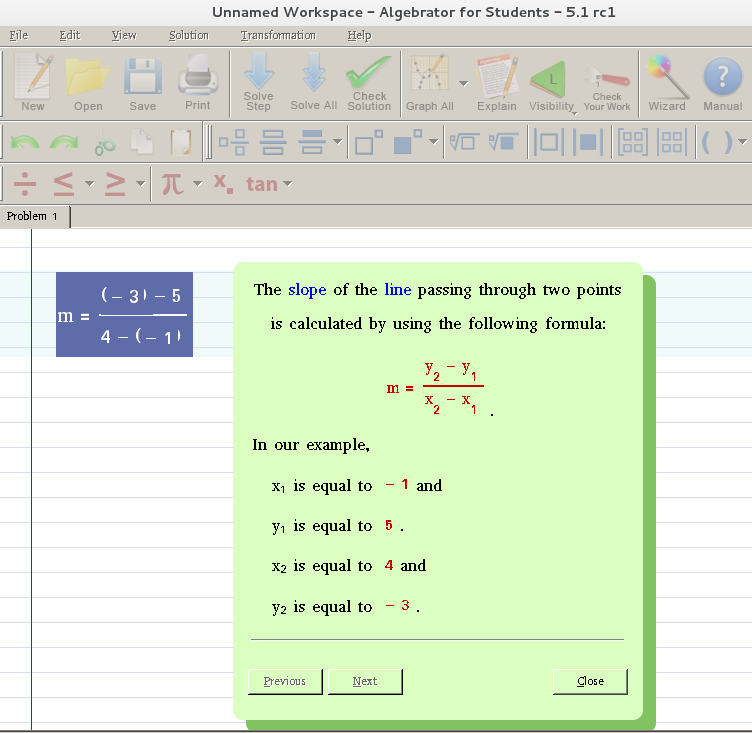
Graph the line passing through the point (1, −1) whose slope is m = (dfrac{3}{4}).
Solution
Plot the given point, (1, −1).
Use the slope formula m = (dfrac{rise}{run}) to identify the rise and the run.
[begin{split} m &= dfrac{3}{4} dfrac{rise}{run} &= dfrac{3}{4} rise &= 3 run &= 4 end{split}]
Starting at the point we plotted, count out the rise and run to mark the second point. We count 3 units up and 4 units right.
Then we connect the points with a line and draw arrows at the ends to show it continues.
We can check our line by starting at any point and counting up 3 and to the right 4. We should get to another point on the line.
Exercise (PageIndex{21}):
Graph the line passing through the point with the given slope:
(2, −2), m = (dfrac{4}{3})
- Answer
Exercise (PageIndex{22}):
Graph the line passing through the point with the given slope:
(−2, 3), m = (dfrac{1}{4})
- Answer
HOW TO: GRAPH A LINE GIVEN A POINT AND A SLOPE
Step 1. Plot the given point.
Step 2. Use the slope formula to identify the rise and the run.
Step 3. Starting at the given point, count out the rise and run to mark the second point.
Step 4. Connect the points with a line.
Example (PageIndex{12}):
Graph the line with y -intercept (0, 2) and slope m = (− dfrac{2}{3}).
Solution
Plot the given point, the y -intercept (0, 2).
Use the slope formula m = rise run to identify the rise and the run.
[begin{split} m &= − dfrac{2}{3} dfrac{rise}{run} &= dfrac{−2}{3} rise &= –2 run &= 3 end{split}]
Starting at (0, 2), count the rise and the run and mark the second point.
Connect the points with a line.
Exercise (PageIndex{23}):
Graph the line with the given intercept and slope:
y-intercept 4, m = (− dfrac{5}{2})
- Answer
Exercise (PageIndex{24}):
Graph the line with the given intercept and slope:

x-intercept −3, m = (− dfrac{3}{4})
- Answer
Example (PageIndex{13}):
Graph the line passing through the point (−1, −3) whose slope is m = 4.
Solution
Plot the given point.
| Identify the rise and the run. | $$m = 4 tag{11.4.44}$$ |
| Write 4 as a fraction. | $$dfrac{rise}{run} = dfrac{4}{1} tag{11.4.45}$$ |
| rise = 4, run = 1 |
Count the rise and run.
Mark the second point. Connect the two points with a line.
Exercise (PageIndex{25}):
Graph the line with the given intercept and slope: (−2, 1), m = 3.
- Answer
Exercise (PageIndex{26}):
Graph the line with the given intercept and slope: (4, −2), m = −2.
2.3 Discover The Slope Of A Linemr. Mac's Page Sheet
- Answer
2.3 Discover The Slope Of A Linemr. Mac's Page Login
Slope is defined as the steepness of a line. Which of the following is a way to remember slope? Slow over Fast Rise over Run If slope is equal to rise over the run, what is the slope of the line? 2/3 3/2 Run =+2 If slope is equal to rise over the run, what is the slope of the line? Run=+3 5/3 -5/3 Find the slope of the line. 2 1/2 Find the slope of the line. undefined slope -10 Find the slope of the line. 3 undefined slope Find the slope of the line. -4/3 -3/4 Undefined Match each graph with the correct slope. Drag each. Positive Negative Zero The slope of a line can be found given two points as well. ∆ Find the slope of the line that passes through the two points (7, 2) and (-4, -6). If the slope is negative, put the negative sign in the m= Find the slope of the line that passes through the points (8, 3) and (2, 9). Find the slope of the line that passes through the points (7, -3) and (-4, 5). If the slope is negative, put the negative sign in the m= Find the slope of the line through (12, 8) and (9, n) is -4/3. Determine the value of n. If the slope is negative, put the negative sign in the Find the slope of the line that passes through the points (-3a, 7a) and (4a, 9a). Find the slope of the line that passes through the points (8, 6) and (-3, -3). If the slope is negative, put the negative sign in the m= When solved for y, a linear equation will be in the form y = mx + b. Remember, m is the slope! The slope of y = -4x + 8 is -4. What is the slope of the linear equation? y = 2 x - 6 m If the slope is negative, put the negative sign in the What is the slope of the linear equation? y = 3/4 x + 9 Solve the equation -x + 2y = 10 for y and then state the slope of the line. If the slope is negative, put the negative sign in the y= Change 4x + y = -7 to slope intercept form. Then tell the slope. y= Change the equation 6x - y = 2 into slope intercept form. Determine the slope. y= |